計算ミス、ケアレスミス、なぜするのか？【原因と対策】

小池です。テスト結果を見て、計算ミス・ケアレスミス・うっかりミス・凡ミス。（今回はケアレスミスという表現にまとめます。）悔しいですよね～。

「自分はケアレスミスが多いんですよね。」
「ケアレスミスがなければ後20点上がって～」

そんな後悔の声を聞きます。じゃあどうすれば防げると思う？「見直しするとか？」

いやいやいやいや。

見直ししないし、しても同じようにミスるんですよ。

ケアレスミスはほとんどがケアレスじゃない

皆がケアレスミスって呼んでいるものは、ほとんどケアレスミスじゃないと思っています。

辞書的には、ケアレス＝注意力不足。

本当は理解していて、解く能力があるという思いが裏側に隠れている感じがしますが、本当にそうですか？

理解していなかったり、能力がなくて間違えていることがほとんどです。

まずケアレスミスにすぎない。本当は自分は解けるのに…という慢心をなくしましょう。

えっ？でも後で解き直したら解けたんですけど…

それは、✕って結果がでたからAという回答は違う。だからBを回答としよう、ってやっているケース。

そして、✕という結果がでたから、これはミスしやすいから普段より丁寧に途中式を書いてやろう、など2回目だから解けているだけです。

最初に一撃でとけなきゃ意味ないですよね。

なぜケアレスミスが永遠になくならないのか？

なぜ間違えたかを細かく掘り下げていないので、永久に同じミスを繰り返します。

問題ごとにミスの原因と、対策は異なります。

例えば、忘れ物が多いとしましょう。私はうっかりしている性格だからさ。と言ってしまえばそれまでです。

忘れ物なんてみんなします。

塾のプリントを忘れる。塾のバッグから出して復習するから。→出したら、塾バックにすぐに戻すことで防げる。

夜寝る前に歯列矯正の器具をつけるのを忘れる。→歯磨きの後に矯正器具をつける流れだから、そのときに思い出しやすいように歯磨きのそばにおいておく。さらに寝室の扉に「矯正つける」って書いて貼っておくとか。

忘れ物も、物によって対策は変わります。

ケアレスミスを防ぐには、問題用紙を見よ

さあ、ここからは実際の生徒のテストのときの問題用紙と、ミスの事例をもとに考えていきましょう。

どうやって分析するか、対策を考えるか一緒に練習していきます。

事例1：単なる引き算のミス？

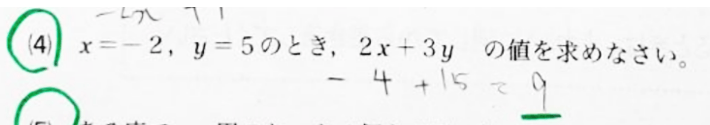
どこで間違えているかわかりますよね？-4+15が本当は11なのに、9になっちゃっているんですね。あー、単なる計算ミス。もったいない！

でほとんどの場合は、話が終わると思うのですが、問題は逆算による確かめ算が習慣化していないことにあります。

引き算って難しいんで、よく間違えるんですよ。小1で習うから引き算は簡単

…ではなく、引き算は難しいんです。

だから、逆算による確かめ算をします。（小学校で習ってますよ。）

9＋4して、13・・・あれ？15にならないな。

・・・

あっ、そっか11が答えか！

って足し算に直して確かめます。脳内で1～2秒でできる作業を怠っているのです。

対策としては、引き算はミスりやすいので、逆算による確かめ算をすることでしょう。

事例2：解き直したら解けるのに…

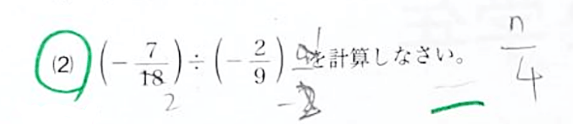
いやー、これ見てどう思います？危ないニオイがプンプンしますね～。

何が危ないか

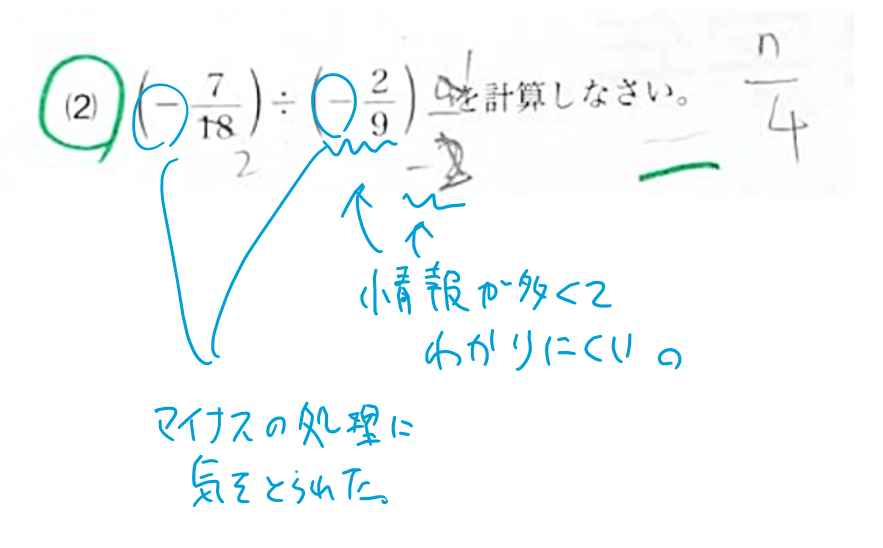
約分しなきゃ、マイナスをミスらないように処理しなきゃ、と2つのことを同時にやるわけです。約分するさいに、-9/2と-2/9が2つ目に入るので、どちらを今使っているかを記憶しておかなければなりません。すると、脳みそが処理することかもう1こ増えて、3このことを同時に処理しています。

ワーキングメモリ（作業記憶）が大きいタイプの子は、これでもミスなく処理できます。勉強を通じてワーキングメモリを広げることは重要なことです。でも、ワーキングメモリが小さいと思うなら、同時に複数処理しなくていいようにしていく必要があります。

良い例

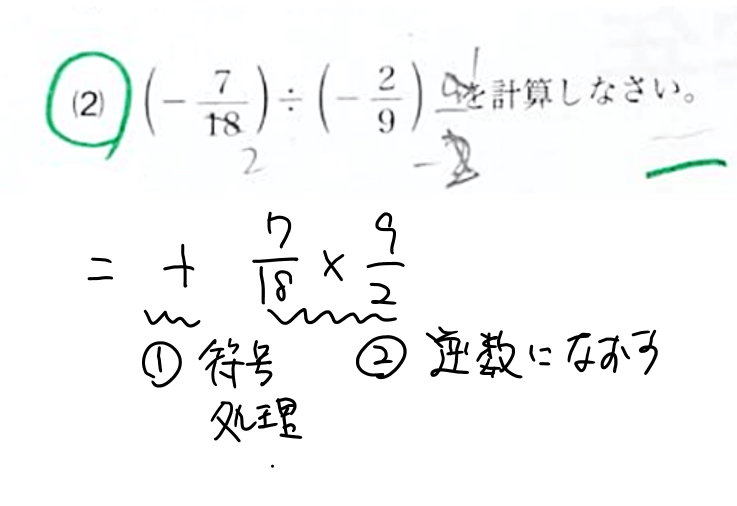
こうやって、

• まずは符号を処理（－÷－→＋）
• ÷の後ろを逆数になおす
• そして約分

1つずつ処理していくことでミスがなくせるでしょう。

この問題のミスの原因は、自分のワーキングメモリの能力を超える処理をしようとした（同時に3つのことをやろうとした。）

短期的対策は、途中式を書くことで1つずつ処理していくこと。

（長期的対策として、あえて途中式を省いてワーキングメモリを鍛えていき、同時に3つ処理することができるようにするのもあり）

事例3：最初に書いた答えのほうがあってたのに…

これは、たぶんミスというより理解していないんじゃないですかね？

• 20より少ない（未満）→20を含まない
• 20以下→20を含む

ですが、≦の書き方を見るに、最初は「＜」と書いて、やっぱ違うかもって不安になって「＝」を下に付け足したように見えます。（イコールだけ不自然に下にあるので）

意味を考えないで表面的に丸暗記しているので、どっちかわからなくなっちゃうのかなと思います。

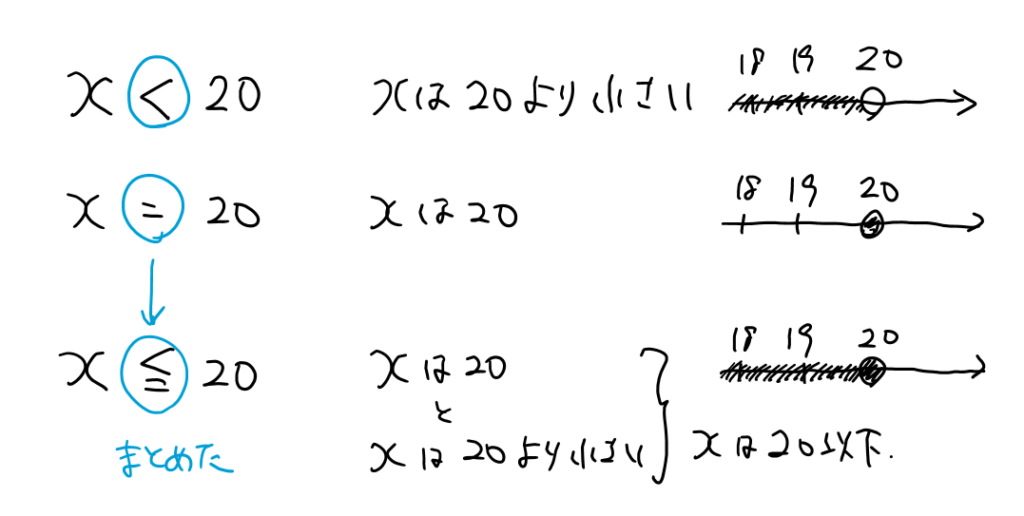
こうかんがればいいかのかなと思います。

本人の話も聞いて、本当のところはどうだったか確かめる必要がありますが、問題用紙だけ見るに疑われるのは理解していない説です。

事例4：えっ？だって、この場合は成り立ちますよ…

おそらく本人はこう考えたんだと思います。頭の中で↓

でも、2、3だったときに成り立たないですよね？

数字を当てはめて、実験して解くのはあっているのですが、書いていないことがマズイとおもいます。

脳内で処理するとつかれるんですよ、脳みそが。

だから、試行回数1になっていて、他の選択肢が浮かばないんです。

3、2なら成り立つけど、2、3だと成り立たないよな？と他の手を考えられていないことがマズイです。

将棋で言えば、あそこに歩を打てばよさそうっ！っていう一見いい手を思いついたときに、それやるとどうなるかを考えずに、パッと思いついた手に飛びついてしまっている感じ。

それを防ぐには、脳みそに負担をかけないように、書きながら考えることでしょうね。

事例5：えっp²じゃないんですか？

p²ってことはp×pなので、例えばp=３だとすると、3²＝9点になっちゃいますね。pが2個ある！二乗だ！って飛びついちゃったんだと思うんですけど、確かめ算ですね。

p=3だとすると、１＋３²だと合計が10点になっちゃって変だな。本当は7点になんなきゃいけないのに。というところでしょう。事例4、事例1と共通点を感じます。

もう1つ気になることが…

普段、塾でこういう指導をしているんですよね。「文字式はみんなミスるから。難しいから。１数字を設定。２式たてて、３文字に戻す。」

それをやっていないんですよね。

ミスの共通点とミスの深堀り

パッと思いついたことに飛びついちゃう

事例4（自然数mとn）、事例5（平均の文字式）に共通しますね。

ボールとバットで合計1100円です。バットはボールより1000円高い。ボールはいくら？

正解は、100円

ではないですよ。

パッと思いついたことに飛びついちゃダメです。

アドバイスされたことを実はやっていない

• 事例1（逆数による確かめ算）→小学校で先生に説明されると思いますがやっていないかと思います。
• 事例5（数字→文字）
• （全体的に）脳内で処理するな！書きながら考えよ！

を実行していない感じがします。

まとめ

ケアレスミスが多いと感じたら、なぜその問題を間違えたのか一問一問深堀りして原因と対策を考えていく必要があります。

• どうしても自分で見ていてもよくわからない
• 自分なりに分析したけどそれがあっているのか不安

という場合には、実物を持ってきて相談に来てください。アドバイスしますよ！

塾生ももちろんですし、塾生出ない方も体験のさいにミスが多くてこの問題のミスの対処はどうすればいいんですか？って問題用紙を見せていただければ相談に乗れます。